1. Basel Face Model

AbstractWe introduce a novel face space model—parametric face drawings (or PFDs)—to generate schematic, though realistic, parameterized line drawings of faces based on the statistical distribution of human facial features. A review of existing face space models (including FaceGen Modeller, Synthetic Faces, MPI, and active appearance model) indicates that current models are constrained by their reliance on ethnically homogeneous face databases. This constraint has led to negative consequences for underrepresented populations, such as impairments in automatized identity recognition of certain demographic groups. Our model is based on a demographically diverse sample of 400 faces (200 female, 200 male; 100 East Asian/Pacific Islander, 100 Latinx/Hispanic, 100 black/African-American, and 100 white/Caucasian) compiled from several face databases (including FERET face recognition technology and the Chicago Face Database).

Each front-view face image is manually coded with 85 landmark points that are then normalized and rendered with MATLAB (MathWorks, Natick, MA) tools to produce a smooth, parameterized face line drawing. We present data from two behavioral experiments to validate our model and demonstrate its applicability. In Experiment 1 we show that PFDs produce a reliable “inversion effect” in short-term recognition, a hallmark of holistic processing.

In Experiment 2, we conduct a celebrity recognition task, comparing performance on PFDs to performance on untextured renderings from FaceGen Modeller. Participants successfully recognized approximately 50% of celebrity faces based on the PFD models, comparable to performance based on FaceGen Modeler (also 50% correct). We highlight a range of potential applications of our model, list some limitations, and provide MATLAB resources for researchers to utilize our face space, including the ability to customize the demographic makeup of the face space, add new faces, and produce morphs and caricatures. Face space (Valentine, ) is theoretical framework wherein individual faces are encoded as points in multidimensional space, where the location of a point provides an appropriate parallel to the mental representation of the corresponding face. Among the assumptions of the face space framework are that (1) the dimensions represent physiognomic features used to encode faces, (2) the Euclidean distance between two points in the space reflects the dissimilarity between the two corresponding faces, (3) the majority of represented faces are own-race faces, (4) the center of face space is densely populated, and (5) the average (or norm) face represents a uniquely neutral face to the individual. Although most researchers agree on these basic assumptions, there are two competing schools of thought about how faces are encoded relative to the norm: norm-based representations (Rhodes, Brennan, & Carey,; Leopold, O'Toole, Vetter, & Blanz, ) and exemplar-based representations (Storrs & Arnold,; Cronin, Spence, Miller, & Arnold, ).

Norm-based representations assume that the norm, or average face, is used explicitly as a reference for coding other faces in the space; each face is thought to be coded as a particular angular deviation from the norm with a particular distance or eccentricity that represents the face's distinctiveness or identity strength. In contrast, exemplar-based representations do not assume that the norm is represented explicitly, but rather arises as a statistical property of the centrally dense distribution of faces. Here, a face is encoded relative to its local neighbors, without explicit reference to a norm (Valentine, ). Since Valentine's theoretical framework was proposed, many studies have tested the degree to which face space is an accurate representation of how faces are organized in a person's own psychological space.

Busey discussed how image processing techniques that allow for morphing between different identities are only useful if the physical image transformations preserve the perceptual relationships between faces. For example, morphing between two “parent” face identities should produce a face that lies in the trajectory between the two parents; however, behavioral ratings and multidimensional scaling (MDS; see Shepard, ) don't bear this out, as morphed faces often lose details of the parent faces due to smoothing artefacts, and thus appear younger, more average, and more attractive than either of the parent faces. Theoretical and physical work by Parke ; Jones and Poggio ; Ezzat and Poggio ; DeCarlos, Metaxas, and Stone ; and Cootes, Edwards, and Taylor created the foundation for a face space. In 1999, Blanz and Vetter created a concrete, “physical” face space by laser scanning real human faces and creating smooth, three-dimensional (3D) models. In their face space, novel face exemplars could be generated from the sample exemplars by separately adjusting the 3D shape and texture parameters. Applying principal components analysis (PCA) to the resulting dimensions produced a set of eigenfaces, candidate dimensions for face representations.

Following Blanz and Vetter's work, other researchers (Wilson, Loffler, & Wilkinson,; Davidenko,; Chang & Tsao, ) have generated physical face space models based on the distribution of “real” face stimuli. Oregon trail 2 online emulator. Although the resulting dimensions vary from study to study, they tend to describe global and configural properties of faces (e.g., adiposity, protrusion of the forehead and chin, distance between the eyes), rather than individual features. Wilson et al. created a “synthetic face space” based on images of real faces. Each face was coded with 37 landmark points based on radial measurements at equally spaced angles around the head (including hairline and head shape).

The low dimensionality of this space facilitated the process of coding faces and describing the underlying dimensions. However, two major limitations of the synthetic face space were the use of generic features (e.g., eyes and mouth) that did not differ across individual faces, and the low number and racial homogeneity of the faces included in the space. Given that the eyes and mouth contribute strongly to face identification (see Schyns, Bonnar, & Gosselin,; Smith, Cottrell, Gosselin, & Schyns, ), this method is limited in its applicability to realistic face recognition behavior. Later, Davidenko created a similar landmark-based face space to describe the variability of profile face silhouettes. This model was based on the manual coding of 18 keypoint locations (36 XY coordinates) on a large number of profile face images.

A PCA revealed the underlying dimensions of the space, and behavioral ratings confirmed that the space can be effectively described by its first 20 dimensions. Although the method did not rely on using prespecified generic facial features, it was limited by the lack of texture information and feature details about the eyes, nose, and mouth. FaceGen Modeller is another popularly used model to create face stimuli, as it allows users to generate realistic 3D faces based on an underlying database of coded faces. Although FaceGen is widely used in research (Oosterhof & Todorov, Hershfield et al., Olivola & Todorov, Davidenko, Vu, Heller, & Collins, ), the method is opaque regarding the independent parameters that define the model. Although FaceGen is based on Blanz and Vetter , the specific methodology and database has not been published. Furthermore, the sampling of faces is highly white-skewed (of the 273 faces, 67.28% are European, 10.66% East Asian, 2.94% South Asian, and 9.56% African).

The inability to modify the database of sampled faces or to inspect the underlying dimensions of the space restricts the model's generalizability, especially for modeling non-white populations. Since then, other researchers have developed more complex and realistic face space models that approach the realism of actual human faces. Recently, Chang and Tsao developed realistic parametrized face stimuli with images of faces from the FEI (Faculty of Industrial Engineering) face database based on the active appearance model (similar to Blanz and Vetter, ). Landmark points were manually coded for each face and smoothed into an outline of the face and key features without textural information. Separate PCAs were performed on the outline shapes and the internal textural information separately, to produce 25 dimensions each, for a total of 50 dimensions. Another recent model, the Diversity in Faces dataset (Merler, Ratha, Feris, & Smith, ) provides a dataset of a million annotated human face images from diverse populations. Although these face spaces provide promising tools for studying facial identity and variation, their main limitation is that other researchers cannot modify the space by adding new faces.

As a result, the resulting face spaces are bound to the populations captured in the model, and cannot be extended by individual researchers to study other face populations, such as infant faces, elderly faces, or specific faces familiar to a participant. The face space we introduce in this paper attempts to address the limitations of the current face spaces available to researchers.

Parametric face drawings (PFDs) are a shape-based parameterization of front-view faces, using a landmark annotation approach similar to the one described in Davidenko. One of the clearest advantages of the PFD space is its availability, ease of use, and customization. Unlike more realistic parametric face spaces (e.g. FaceGen, and Chang & Tsao, ), the PFD can be easily modified or expanded by individual researchers by adding or removing faces and manually coding new faces into the space.

Critically, because PFDs are not sensitive to textural information, researchers can add any front view face to the space, regardless of lighting conditions or other image properties that typically constrain complex texture-based face space. In addition, we have released the source code for encoding new face stimuli into the model and rendering arbitrary faces for experimental study. Our model is fully available online, and instructions for coding new faces are provided on the Open Science Framework (OSF). Finally, because the renderings are shape-based and do not include complex texture information, PFDs address the limitations raised by Busey ; when creating caricatures or morphs between two identities, the resulting faces do not suffer from blending artefacts associated with other models that include texture.

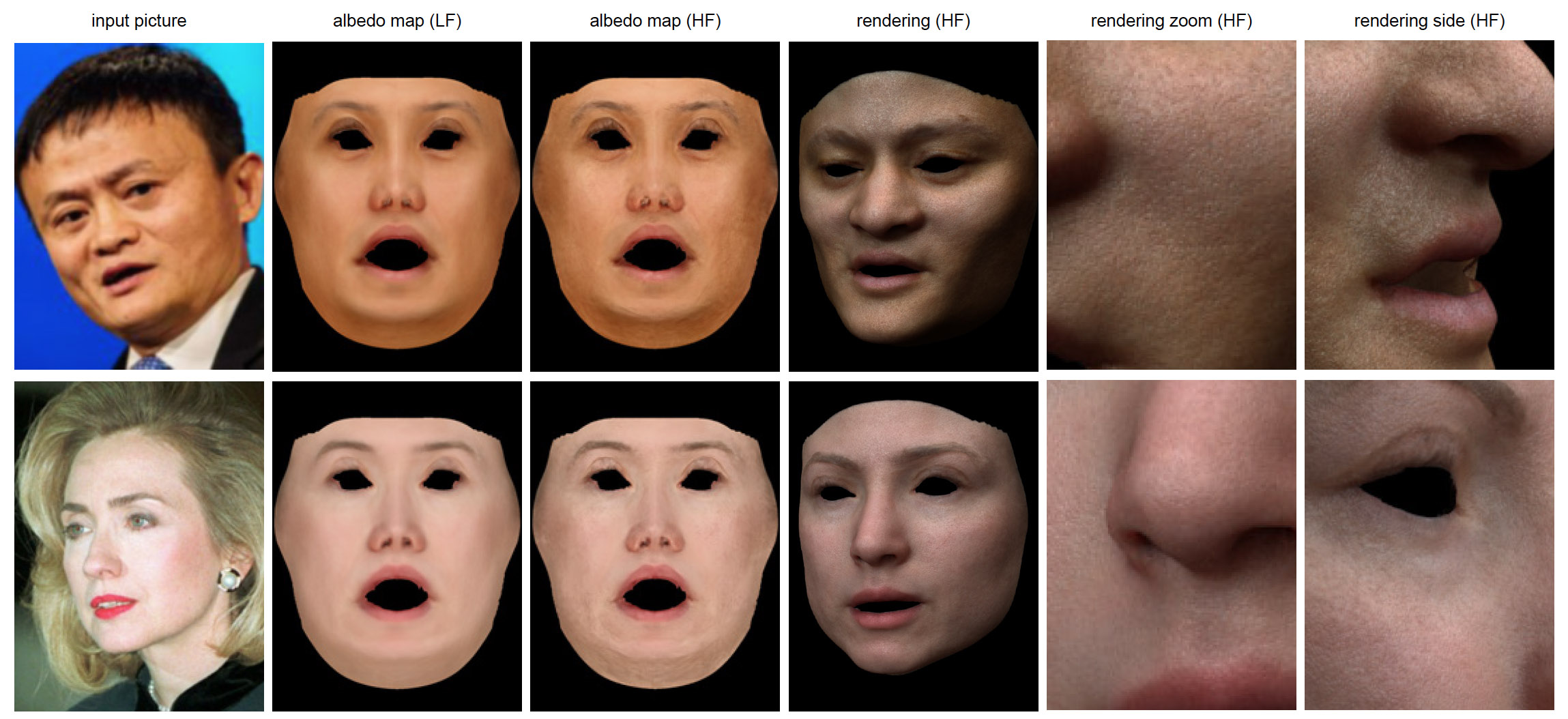
A further advantage of using lines to represent facial regions and features is an increased tolerance of caricatures; that is caricatures and “extreme” faces can be created without unrealistic image artefacts due to morphing texture information. In the discussion we also describe the benefits of this model for studying face drawing (see also Day & Davidenko, ). PFDs are rendered as smooth line drawings that include the outline of the face, the eyes, eyebrows, nose, and mouth (see ). The space is constructed based on 400 face identities, each of which has been manually coded by research assistants by identifying 85 keypoints. The set of 85 key points were chosen based on pilot studies that evaluated the recognizability of celebrity faces based on different number of points (see Day & Davidenko, ). After the 85 points are coded, their coordinates are normalized to a standard position by scaling, rotation, and translation, such that the two pupils are located at 0,0 and 2,0. After excluding the noninformative pupil points, the coordinates of the remaining 83 keypoints (166 x-y values) are rendered using MATLAB graphing functions to spline, fill, and plot individual features and create a parametric face drawing (PFD; see ).

The distribution of 166 informative x-y coordinates across the 400 faces is entered into a PCA to reveal orthogonal dimensions that best explain the variability of the face exemplars. Importantly, the renderings do not rely on any texture information present in the face image.

As such, any front-facing face image is a candidate for inclusion in the face space. The face identities included in our PFD model are sampled from the following: FERET, Utrecht face database, Mugshot database, 10k U.S. Adult Faces Database, Chicago Face Database, and pictures of University of California, Santa Cruz, (UCSC) students, chosen to represent a demographically diverse sample of faces. The space is equally balanced between male and female faces, and across four racial groups; East Asian/Pacific Islander, Latinx/Hispanic, black/African-American, and white/Caucasian. The sample includes adult faces (18–65 years of age, with a mean age of 30.7 years), although the distribution of ages is not equal across all races and genders. The balanced distribution of gender and race results in face-space dimensions (principal components, or PCs) that are representative of all groups equally, rather than biased toward white/Caucasian faces, which is the case in practically all existing face space models. Shows the effects of varying the coefficients of the first 6 PCs in the rendered faces.

Shows the distribution of faces along the first 2 PCs based on gender and race. On the OSF page for this project , we provide MATLAB tools for rendering PFDs; constructing averages, morphs, and caricatures; generating new identities; and computing the variability within and across groups of faces. An individual face can be represented as a single point in the 166-dimensional face space, as an “identity vector” of PC coefficients. An all-0 vector represents the average face, and caricatures can be constructed by scaling identity vectors away from the average face (see ). Morphs can be constructed as weighted sums of “parent” faces. Because PFDs do not carry texture information, morphs are not vulnerable to blending artefacts present in other models.

Finally, PFDs are also generative, allowing researchers to easily construct realistic identities based on the distribution of existing faces. Because the PCA dimensions are normally distributed, new faces can be generated by assigning normally distributed random values to each of the 166 dimensions, scaled by the standard deviation of each PC, which creates artificial but realistic looking faces (see ). Although the space has 166 dimensions (based on the x-y coordinates of the 83 informative key points), shows that face identities are very well characterized with just the first 60 dimensions. Therefore, the PFD face space is approximately 60-dimensional for practical purposes. The utility of a face space depends largely on the perceptual properties of the stimuli.

As such, we describe in the following section two experiments intended to validate the PFD stimuli. In Experiment 1, we present data from a short-term recognition task, and demonstrate that PFDs elicit a face inversion effect, a hallmark phenomenon of face processing.

In Experiment 2, we assess the amount of personally identifiable information in PFDs by conducting a celebrity recognition study. Our results indicate that PFDs do provide identity information, comparable to that available in the popular FaceGen model based on texture-less renderings.

In each trial, participants were shown one of the three faces in a vertex group. This served as the target face to be recognized following a short delay. Each target face was presented either in an upright or inverted orientation for 2 seconds, followed by a jumbled mask for 0.25 seconds and 1.25 second blank interstimulus interval, after which all three vertex faces from the set were presented to the participant in a random arrangement on the screen. The orientation of the three vertex faces was always congruent with that of the studied face, and this was randomly assigned across trials. The three vertex faces stayed on the screen until the participant indicated which one they had previously seen, by pressing the 1, 2, or 3 on the keyboard.

The experiment began with three practice trials, where participants were given feedback on their choices. After the three practice trials, the participant completed 80 real trials with no feedback, which included 40 upright trials, and 40 inverted trials, in a random order. We measured performance and reaction time on correct trials.

We found that there was significantly higher accuracy when faces were upright ( M = 0.7715, SD = 0.0926) over inverted ( M = 0.7184, SD = 0.0969), t(32) = 3.777, p = 0.00065 (see, left panel). We also found significantly shorter reaction times on correct trials for upright faces ( M = 2.2142, SD = 0.4092) over inverted ( M = 2.3695, SD = 0.5675), t(32) = -2.4149, p = 0.0216 (, right panel). Together, these results show that people are faster and more accurate at identifying upright faces. This robust inversion effect replicates the hallmark finding and supports the use of PFDs as face stimuli for research. We found a reliable inversion effect: participants were better and faster at recognizing upright PFDs than inverted PFDs. The inversion effect indicates that PFD stimuli are processed similarly to faces. The relatively modest effect on performance may be due in part to the nature of PFD stimuli.

The faces are rendered as line drawings, which primarily represent high spatial frequency information. Goffaux and Rossion demonstrated that holistic face processing depends in part on low spatial frequencies. Thus the face inversion effect (which interrupts holistic processing) is likely attenuated by high spatial frequency content in PFD stimuli.

The experiment consisted of a face-to-name matching task using 16 well-known celebrity faces (eight females and eight males). Each participant attempted to recognize eight PFDs, eight FaceGen faces, and then all 16 grayscale photographs to serve as a baseline measure. The order in which PFDs and FaceGen faces were presented was counterbalanced across participants, as well as which eight faces were assigned to be shown in PFD or FaceGen format. To construct the PFDs, photographs of popular celebrity identities were manually coded by research assistants and rendered in MATLAB. FaceGen stimuli were similarly created by uploading the same celebrity photographs into the FaceGen Modeller program, labeling key points, and rendering the faces as an untextured 3D volume. All images (PFDs, FaceGen, and photographs) were shown in grayscale.

Participants were asked to complete three sheets of an identity recognition task on paper (materials available here: ). On each sheet, participants were asked to match the celebrity faces (either PFDs, FaceGen, or grayscale images) with their full names.

There were four possible orders of presentation, counterbalanced across participants: (1) the first half of the face identities shown first as PFDs and the second half as FaceGen stimuli, (2) the first half of the face identities shown first as FaceGen stimuli and the second half as PFDs, (3) the second half of the face identities shown first as PFDs and the first half as FaceGen stimuli, or (4) the second half of the face identities shown first as FaceGen stimuli and the first half as PFDs. The 16 grayscale photographs were always shown last, and participants were asked to identify all of them to provide a baseline score. A one-way repeated measures analysis of variance with a factor of face format (three levels: PFD, FaceGen, photographs) revealed a significant effect of face format on recognition performance F(2, 152) = 65.3, p. Our results showed that participants performed equally well with PFDs and FaceGen faces on a celebrity recognition task, both substantially above chance levels. The two renderings of face stimuli are created with very different visual information: PFDs are rendered primarily with high spatial frequency (HSF) information, whereas FaceGen faces are rendered as smooth 3D volumes. Nevertheless, we found that PFDs preserve and display identity information to a similar degree as FaceGen renderings.

These results suggest PFDs are viable stimuli for identity recognition experiments. Our experiments with PFDs worked to establish them as viable stimuli for face experiments. The results of Experiment 1 demonstrated a robust inversion effect with PFDs, with upright PFDs being recognized more accurately and faster than inverted PFDs.

Experiment 2 further provided evidence that PFDs provide identity information at a level comparable to the popularly used FaceGen Modeller faces. Therefore PFDs can be used in a wide array of face perception experiments and applications, as discussed as follows. We propose that PFDs provide three main benefits compared to existing face space models: demographic diversity, accessibility and customizability of the model, and the simplicity and flexibility of a shape-based rendering. First, they are based on a demographically diverse sample of faces. Although this should be standard practice in the face perception field, current models are highly ethnically biased, with popular models such as FaceGen being based primarily on white/Caucasian faces.

This bias creates problems, such as low-fidelity representation of faces from underrepresented groups. By providing a face space that is equally balanced across four major racial groups, PFD provides a new platform for researchers interested in understanding face recognition across a more diverse population of observers. A second key advantage of PFDs as experimental stimuli includes the accessibility of the model and flexibility to add new faces into the model. Any front-view face image is a candidate to be encoded into the space, regardless of the particular lighting conditions or image properties. This makes it straightforward for researchers to expand the face space as needed to study face processing in specific demographic groups, as well as to investigate questions of other-race face recognition.

The ability to add new faces to the space regardless of lighting, color, or texture information represents increased flexibility for customizing a face space compared to existing models. Researchers can construct their own face spaces to reflect the demographic distribution of the population they are studying. We have made PFDs that are free and available online for face perception researchers. The public database includes demographic information (age, gender, and race) the XY coordinates of the 85 keypoints, and PC coefficients for each of the 400 faces included in the database. In addition, we provide MATLAB scripts for rendering faces and for removing or adding new faces to the space.

As mentioned earlier, any front-view face (regardless of lighting, color, size, or textural information) can be added to the space, allowing for the creation of diverse and inclusive face space models. Finally, the simple, shape-based parameterization avoids issues of blending artefacts associated with more complex texture-based models. Novel PFDs can be generated by modifying an existing identity (e.g., caricaturing), combining multiple identities (i.e., morphing), or randomly generating new identities by sampling normally distributed values for the coefficients of the principal components. The use of simple lines, curves, and bounded shapes to represent features and facial regions allows the creation of morphs that do not have blending issues that otherwise contribute to perceptual judgments of increased attractiveness and decreased age in morphs. As a result, PFDs have increased tolerance for caricaturing, allowing for further deviations of a face away from the average without “breaking” the face information. One innovative benefit of shape based models is their application to the study of face drawings. The simplicity of PFD stimuli allows for even novice artists to draw them accurately.

We recently demonstrated this in a drawing study, where we showed that novice participants are able to more accurately copy upright PFDs compared to inverted PFDs, supporting the view that holistic processing aids in drawing (Day & Davidenko, ). Here, the line-based nature of PDFs served as an ideal model for drawing, eliminating complex texture-to-line transformations that typically hinder the accuracy of drawings for novices. In addition, the model provided a direct objective measure of drawing accuracy. By comparing the face-space distances between target and drawn faces, we could compute a physical measure of accuracy which correlated with perceptual ratings. Future studies can expand on this paradigm to study how and whether novice participants can be trained to draw PFD faces from memory, which would provide a new avenue of research in face reconstruction. Although the simple, shape-based parameterization can be seen as a methodological advantage, it also carries some limitations. The two main limitations of PFDs as experimental stimuli include (1) the manual coding process and (2) the absence of some important visual properties of faces such as texture, color, and depth information.

We list the manual coding of faces as a limitation due to the time cost and possible subjectivity in coding the landmark points. Each face includes 85 landmark points that need to be hand-coded by trained face coders, which takes between 5 and 10 minutes, depending on the coder's experience. To address this limitation, we suggest that this model could be extended to automate the coding of landmark points. Previous work in this field (e.g., Samal & Iyengar,; Jafri & Arabnia,; Amos, Ludwiczuk, & Satyanarayanan, ) has produced algorithms that automatically detect these landmark points. Another limitation is that PFDs do not have all the visual properties that faces do.

Since they are coded and rendered as outlines and filled bounded shapes, there is a lack of textural and color information. As such, PFDs preserve HSF information well but do not preserve medium spatial frequency (MSF) or low spatial frequency (LSF) information. The lack of MSFs and LSFs could interfere with some aspects of face processing, such as holistic processing (Goffaux & Rossion, ). We also note the lack of hair information as a limitation for identity recognition, but like most face models we excluded hair information to decrease the dimensionality of the space and allow for seamless morphing between faces. Despite these limitations, there are many possible applications of the PFD face space model.

As discussed previously, a primary benefit of the space is that researchers can customize and add to the space as needed to create representative face spaces for the population they study. For example, a researcher in a largely Hispanic population can customize the space so that it includes more Latinx faces compared to the other race groups. The resulting dimensions of the space will then reflect the distribution of that particular population (e.g., resulting face-space dimensions will be those that best differentiate faces from that population). Furthermore, the face space allows researchers to calibrate the variability of different groups of faces so that, for instance, black faces are equally variable as white faces when studying the other race effect (Malpass & Kravitz, ). The space also allows us to address questions that have to do with variability across sets of faces.

For example, what accounts for more variation in face identity—gender or race? Are the dimensions that correlate with gender the same (or similar) across races? Is the variability across male and female faces comparable in different ethnic groups?

FIGURE 1 The same individual imaged with the same camera and with nearly the same facial expression and pose may appear dramatically different with changes in lighting conditions. The first two images were taken indoors; the third and fourth images were taken outdoors. All four images were taken with a Canon EOS 1D digital camera.

Before each picture was taken, the subject was asked to make a neutral facial expression and to look directly into the lens.“Variations between the images of the same face due to illumination and viewing direction are almost always larger than image variations due to changes in face identity” (Moses et al., 1994). As shows, the same person, with the same facial expression, can appear strikingly different with changes in the direction of the light source and point of view. These variations are exacerbated. By additional factors, such as facial expression, perspiration, hair style, cosmetics, and even changes due to aging.The problem of face recognition can be cast as a standard pattern-classification or machine-learning problem. Imagine we are given a set of images labeled with the person’s identity (the gallery set) and a set of images unlabeled from a group of people that includes the individual (the probe set), and we are trying to identify each person in the probe set.

This problem can be attacked in three steps. In the first step, the face is located in the image, a process known as face detection, which can be as challenging as face recognition (see Viola and Jones, 2004, and Yang et al., 2000, for more detail). In the second step, a collection of descriptive measurements, known as a feature vector, is extracted from each image. In the third step, a classifier is trained to assign a label with a person’s identity to each feature vector. (Note that these classifiers are simply mathematical functions that return an index corresponding to a subject’s identity.)In the last few years, numerous feature-extraction and pattern-classification methods have been proposed for face recognition (Chellappa et al., 1995; Fromherz, 1998; Pentland, 2000; Samil and Iyengar, 1992; Zhao et al., 2003). Geometric, feature-based methods, which have been used for decades, use properties and relations (e.g., distances and angles) between facial features, such as eyes, mouth, nose, and chin, to achieve recognition (Brunelli and Poggio, 1993; Goldstein et al., 1971; Harmon et al., 1978, 1981; Kanade, 1973, 1977; Kaufman and Breeding, 1976; Li and Lu, 1999; Samil and Iyengar, 1992; Wiskott et al., 1997). Pose, and with a particular expression is reliable only if the face has been previously seen under similar circumstances.

In fact, variations in appearance between images of the same person confound appearance-based methods. To demonstrate just how severe this variability can be, an array of images shows variability in the Cartesian product of pose × lighting for a single individual.If the gallery set contains a very large number of images of each subject in many different poses, lighting conditions, and with many different facial expressions, even the simplest appearance-based classifier might perform well. However, there are usually only a few gallery images per person from which the classifier must learn to discriminate between individuals.In an effort to overcome this shortcoming, there has been a recent surge in work on 3-D face recognition. The idea of these systems is to build face-recognition systems that use a handful of images acquired at enrollment time to estimate models of the 3-D shape of each face. The 3-D models can then be used to render images of each face synthetically in novel poses and lighting conditions—effectively expanding the gallery set for each face. Alternatively, 3-D models can be used in an iterative fitting process in which the model for each face is rotated, aligned, and synthetically illuminated to match the probe image. Conversely, the models can be used to warp a probe image of a face back to a canonical frontal point of view and lighting condition.

In both of these cases, the identity chosen corresponds to the model with the best fit.The 3-D models of the face shape can be estimated by a variety of methods. In the simplest methods, the face shape is assumed to be a generic average of a large collection of sample face shapes acquired from laser range scans. Georghiades and colleagues (1999, 2000) estimated the face shape from changes in the shading in multiple enrollment images of the same face under varying lighting conditions. Kukula (2004) estimated the shape using binocular stereopsis on two enrollment images taken from slightly different points of view. Ohlhorst (2005) based the estimate on deformations in the grid pattern of infrared light projected onto the face. In another study, Blanz and Vetter (2003) inferred the 3-D face shape from the shading in a single image using a parametric model of face shape.

Often, a “bootstrap” set of prior training data of face shape and reflectance taken from individuals who are not in the gallery or probe sets is used to improve the shape and reflectance estimation process.The 3-D face recognition techniques described above constitute just a small sampling of the work going on in this area, much of it too new to appear in surveys. To give the reader an idea of the potential of these approaches, the seven images (, top row) under variable lighting conditions are used to estimate the face shape and reflectance. The estimate is then used to synthesize images of the face under the same conditions as those shown in. Note that much of the variation in appearance in pose and lighting can be inferred from as few as nine gallery images. FIGURE 3 A variation of photometric stereopsis was used to compute the shape and reflectance of the face in the bottom row based on the seven gallery images in the top row. Source: Georghiades et al., 1999. Reprinted with permission.Although recent advances in 3-D face recognition have gone a long way toward addressing the complications causes by changes in pose and lighting, a great deal remains to be done.

Natural outdoor lighting makes face recognition difficult, not simply because of the strong shadows cast by a light source such as the sun, but also because subjects tend to distort their faces when illuminated by a strong light; compare again the indoor and outdoor expressions of the subject in. Furthermore, very little work has been done to address complications arising from voluntary changes in facial expression, the use of eyewear, and the more subtle effects of aging. The hope, of course, is that many of these effects can be modeled in much the same way as face shape and reflectance and that recognition will continue to improve in the coming decade. REFERENCESBlanz, V., and T. Face recognition based on fitting a 3D morphable model. IEEE Transactions in Pattern Analysis and Machine Intelligence 25(9): 1063–1074.Brunelli, R., and T.

Face recognition: features vs templates. IEEE Transactions in Pattern Analysis and Machine Intelligence 15(10): 1042–1053.Chellappa, R., C. Wilson, and S.

Human and machine recognition of faces: a survey. Proceedings of the IEEE 83(5): 705–740.Cox, I., J. Ghosn, and P. Feature-Based Face Recognition Using Mixture Distance. 209–216 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Fromherz, T. Face Recognition: A Summary of 1995–1997.

ICSI TR-98-027. Berkeley, Calif.: International Computer Science Institute, University of California, Berkeley.Georghiades, A., P.

Belhumeur, and D. Illumination-Based Image Synthesis: Creating Novel Images of Human Faces under Differing Poses and Lighting. 47–54 in Proceedings of the IEEE Workshop on Multi-View Modeling and Analysis of Visual Scenes.

New York: IEEE.Georghiades, A., P. Belhumeur, and D. From Few to Many: Generative Models for Recognition under Variable Poses and Illumination. 277–284 in Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition. New York: IEEE.Georghiades, A., P. Belhumeur, and D.

From Few to Many: Illumination Cone Models for Face Recognition under Variable Lighting and Poses. IEEE Transactions in Pattern Analysis and Machine Intelligence 23(6): 643–660.Goldstein, A., L. Harmon, and A. Identification of human faces.

Proceedings of the IEEE 59(5): 748–760.Hallinan, P. A Low-Dimensional Representation of Human Faces for Arbitrary Lighting Conditions. 995–999 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.

New York: IEEE.Hallinan, P. A Deformable Model for Face Recognition under Arbitrary Lighting Conditions. Thesis, Harvard University. Unpublished.Hallinan, P., G. Yuille, and D.

Two- and Three-Dimensional Patterns of the Face. Wellesley, Mass.: A.K. Peters.Harmon, L., S. Ramig, and U. Identification of human face profiles by computer. Pattern Recognition 10(5-6): 301–312.Harmon, L., M. Lasch, and P.

Machine identification of human faces. Pattern Recognition 13(2): 97–110.Kanade, T.

Picture Processing by Computer Complex and Recognition of Human Faces. Thesis, Kyoto University. Unpublished.Kanade, T. Computer Recognition of Human Faces. Stuttgart, Germany: Birkhauser Verlag.Kaufman, G., and K. The automatic recognition of human faces from profile silhouettes.

IEEE Transactions on Systems, Man and Cybernetics 6(February): 113–121.Kukula, E. Effects of Light Direction on the Performance of Geometrix FaceVision® 3D Face Recogntion System. Proceedings of the Biometrics Consortium Conference. Gaithersburg, MD: NIST.

Available online at:.Li, S., and J. Face recognition using nearest feature line.

IEEE Transactions on Neural Networks 10(2): 439–443.Moghaddam, B., and A. Probabilistic visual learning for object representation. IEEE Transactions on Pattern Analysis and Machine Intelligence 19(7): 696–710.Murase, H., and S. Visual learning and recognition of 3-D objects from appearance. International Journal of Computer Vision 14(1): 5–24. Biometrics Security Solutions Are Here from the Future. Available online at: (April 26, 2005).Pentland, A.

Looking at people: sensing for ubiquitous and wearable computing. IEEE Transactions on Pattern Analysis and Machine Intelligence 22(1): 107–119.Pentland, A., B. Moghaddam, and T.

View-Based and Modular Eigenspaces for Face Recognition. 84–91 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Poggio, T., and K. Example-based learning for view-based human face detection. II: 843–850 in Proceedings of the ARPA Image Understanding Workshop. Arlington, Va.: DOD.Samal, A., and P. Automatic recognition and analysis of human faces and facial expressions: a survey.

Pattern Recognition 25(1): 65–77.Sirovich, L., and M. Low-dimensional procedure for the characterization of human faces. Journal of the Optical Society of America A4(3): 519–524.Turk, M., and A.

Eigenfaces for recognition. Journal of Cognitive Neuroscience 3(1): 71–96.Viola, P., and M.J.

Robust real-time face detection. International Journal of.

Basel Face Model

Computer Vision 57(2): 137–154.Wiskott, L., J. Kruger, and C. Von der Malsburg. Face recognition by elastic bunch graph matching.

IEEE Transactions on Pattern Analysis and Machine Intelligence 19(7): 775–779.Yang, M., N. Ahuja, and D.

Face Detection Using a Mixture of Linear Subspaces. 70-76 in Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition. New York: IEEE.Zhao, W., R. Chellappa, P.J. Phillips, and A.

Face recognition: a literature survey. Association for Computing Machinery Computer Survey 35(4): 399–458. BIBLIOGRAPHYBelhumeur, P.N., and D. What is the set of images of an object under all possible illumination conditions? International Journal of Computer Vision 28(3): 245–260.Belhumeur, P.N., J.P. Hespanha, and D J. Eigenfaces vs.

Fisherfaces: recognition using class-specific linear projection. IEEE Transactions on Pattern Analysis and Machine Intelligence 19(7): 711–720. Special Issue on Face Recognition.Belhumeur, P.N., D. Kriegman, and A.

The Bas-Relief Ambiguity. 1040–1046 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Beymer, D. Face Recognition under Varying Poses.

756–761 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Beymer, D., and T.

Face Recognition from One Example View. 500–507 in Proceedings of the IEEE International Conference on Computer Vision. New York: IEEE.Blanz, V., and T. A Morphable Model for the Synthesis of 3D Faces. 187–194 in Proceedings of the 26th Computer Graphics and Interactive Techniques/International Conference on Computer Graphics and Interactive Techniques (SIGGRAPH 1999). New York: ACM Press/Addison-Wesley.Chen, H., P. Belhumeur, and D.

In Search of Illumination Invariants. 254–261 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Chen, Q., H. Face Detection by Fuzzy Pattern Matching.

591–596 in Proceedings of the IEEE International Conference on Computer Vision. New York: IEEE.Cootes, T., G. Edwards, and C. Active Appearance Models. 484–498 in Proceedings of the European Conference on Computer Vision, vol.

Berlin: Springer. Cootes, T., K. Walker, and C.

View-Based Active Appearance Models. 227–232 in Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition. New York: IEEE.Craw, I., D. Finding Face Features. 92–96 in Proceedings of the European Conference on Computer Vision. Berlin: Springer.Edwards, G., T.

Cootes, and C. Advances in Active Appearance Models. 137–142 in Proceedings of the IEEE International Conference on Computer Vision. New York: IEEE.Epstein, R., P. Hallinan, and A.

5±2 Eigenimages Suffice: An Empirical Investigation of Low-Dimensional Lighting Models. In IEEE Physics Based Modeling Workshop in Computer Vision, Session 4.

New York: IEEE.Frankot, R.T., and R. A method for enforcing integrability in shape from shading algorithms. IEEE Transactions on Pattern Analysis and Machine Intelligence 10(4): 439–451.Georghiades, A., D. Kriegman, and P.

Illumination Cones for Recognition under Variable Lighting: Faces. 52–59 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Govindaraju, V. Locating human faces in photographs.

International Journal of Computer Vision 19(2): 129–146.Hayakawa, H. Photometric stereo under a light-source with arbitrary motion.

Journal of the Optical Society of America 11A(11): 3079–3089.Horn, B. Computer Vision. Cambridge, Mass.: MIT Press.Huang, F., Z. Zhang, and T. Pose Invariant Face Recognition.

245–250 in Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition. New York: IEEE.Jacobs, D.

Linear Fitting with Missing Data: Applications to Structure from Motion and Characterizing Intensity Images. 206-212 in Procedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Juell, P., and R. A hierarchical neural-network for human face detection. Pattern Recognition 29(5): 781–787.Lambert, J. Photometria Sive de Mensura et Gradibus Luminus, Colorum et Umbrae.

Augsberg, Germany: Eberhard Klett.Lanitis, A., C. Taylor, and T. A Unified Approach to Coding and Interpreting Face Images.

368–373 in Proceedings of the IEEE International Conference on Computer Vision. New York: IEEE.Lanitis, A., C. Taylor, and T. Automatic interpretation and coding of face images using flexible models.

IEEE Transactions in Pattern Analysis and Machine Intelligence 19(7): 743–756.Lee, C., J. Automatic human face location in a complex background using motion and color information. Pattern Recognition 29(11): 1877–1889.Leung, T., M. Finding Faces in Cluttered Scenes Using Labeled Random Graph Matching.

537–644 in Proceedings of the IEEE International Conference on Computer Vision. New York: IEEE.Li, Y., S. Support Vector Regression and Classification Based Multi-view Face Detection and Recognition. 300–305 in Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition. New York: IEEE.Moghaddam, B., and A. Probabilistic Visual Learning for Object Detection. 786–793 in Proceedings of the IEEE International Conference on Computer Vision.

New York: IEEE.Moses, Y., Y. Adini, and S. Face Recognition: The Problem of Compensating for Changes in Illumination Direction. 286–296 in Proceedings of the European Conference on Computer Vision.

Berlin: Springer. Nayar, S., and H. Dimensionality of Illumination Manifolds in Appearance Matching. 165 in Proceedings of the International Workshop on Object Representation and Computer Vision. London, UK: Springer-Verlag.O’Toole, A., T. Sex classification is better with three-dimensional head structure than with texture.

Perception 26: 75–84.Phillips, P., H. Rauss, and S.

The FERET Evaluation Methodology for Face-Recognition Algorithms. 137–143 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Phillips, P., H. Huang, and P. The FERET database and evaluation procedure for face recognition algorithms. Image and Visual Computing 16(5): 295-306.Riklin-Raviv, T., and A.

The Quotient Image: Class Based Recognition and Synthesis under Varying Illumination Conditions. II: 566–571 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Rowley, H., S. Baluja, and T. Neural network-based face detection. IEEE Transactions on Pattern Analysis and Machine Intelligence 20(1): 23–38.Rowley, H., S. Baluja, and T.

Rotation Invariant Neural Network-Based Face Detection. 38–44 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE.Samil, A., and P. Human face detection using silhouettes. Pattern Recognition and Artificial Intelligence 9: 845–867.Shashua, A. Geometry and Photometry in 3D Visual Recognition. Thesis, Massachusetts Institute of Technology.

Unpublished.Shashua, A. On photometric issues in 3D Visual Recognition from a Single 2D Image. International Journal of Computer Vision 21(1–2): 99–122.Shum, H., K. Ikeuchi, and R. Principal component analysis with missing data and its application to polyhedral object modeling.

IEEE Transactions in Pattern Analysis and Machine Intelligence 17(9): 854–867.Silver, W. Determining Shape and Reflectance Using Multiple Images. Thesis, Massachusetts Institute of Technology. Unpublished.Tomasi, C., and T. Shape and motion from image streams under orthography: a factorization method.

International Journal of Computer Vision 9(2): 137–154.Vetter, T. Synthesis of novel views from a single face image. International Journal of Computer Vision 28(2): 103–116.Vetter, T., and T. Linear object classes and image synthesis from a single example image. IEEE Transactions on Pattern Analysis and Machine Intelligence 19(7): 733–742.Woodham, R. Analysing images of curved surfaces. Artificial Intelligence 17: 117–140.Yang, M., D.J.

Kriegman, and N. Detecting faces in images: a survey. IEEE Transactions on Pattern Analysis and Machine Intelligence 24(1): 34–58.Yow, K., and R. Feature-based human face detection. Image Visual Computing 15(9): 713–735.Yu, Y., and J.

Recovering photometric properties of architectural scenes from photographs. Computer Graphics (SIGGRAPH 1998 Conference Proceedings) 32: 207–217.Yuille, A., and D. Shape and Albedo from Multiple Images Using Integrability. 158–164 in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.

New York: IEEE.Zhao, W., and R. SFS Based View Synthesis for Robust Face Recognition. 285–292 in Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition. New York: IEEE.Zhao, W., R. Chellappa, and P.

Subspace Linear Discriminant Analysis for Face Recognition. College Park, Maryland: Center for Automation Research, University of Maryland. Contents. i–xii. 1–4. 5–14.

15–22. 23–32.

33–36. 37–44. 45–52. 53–58. 59–68. 69–74.

75–82. 83–88. 89–98. 99–108. 109–112. 113–118.

119–130. 131–142. 143–152. 153–166. 167–176. 177–180.

181–190. Welcome to OpenBook!You're looking at OpenBook, NAP.edu's online reading room since 1999. Based on feedback from you, our users, we've made some improvements that make it easier than ever to read thousands of publications on our website.Do you want to take a quick tour of the OpenBook's features?.Show this book's table of contents, where you can jump to any chapter by name.or use these buttons to go back to the previous chapter or skip to the next one.Jump up to the previous page or down to the next one. Also, you can type in a page number and press Enter to go directly to that page in the book.Switch between the Original Pages, where you can read the report as it appeared in print, and Text Pages for the web version, where you can highlight and search the text.To search the entire text of this book, type in your search term here and press Enter.Share a link to this book page on your preferred social network or via email.View our suggested citation for this chapter.Ready to take your reading offline?

Click here to buy this book in print or download it as a free PDF, if available.